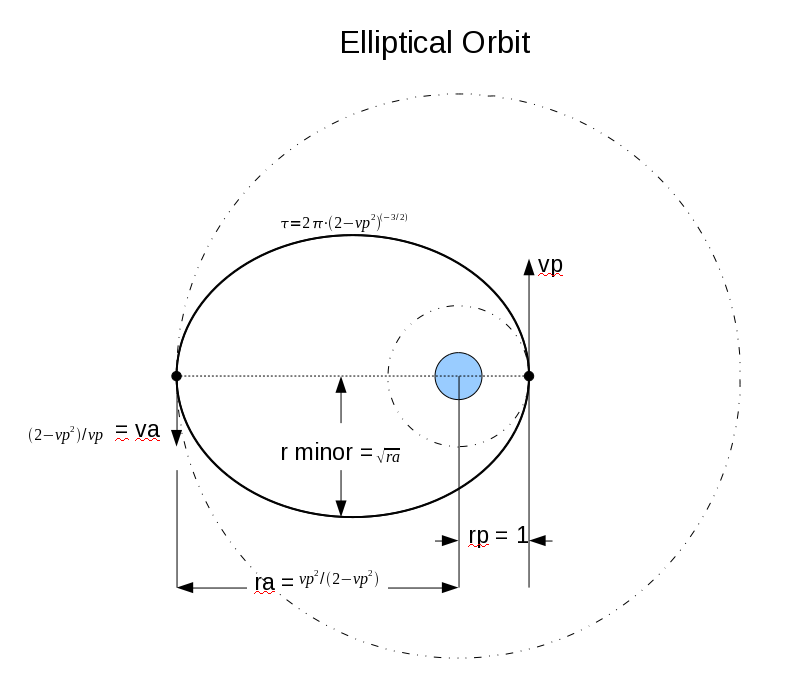
A small satellite orbiting a large mass will maintain a circular orbit if the force of gravity, G·m1·m2 / r^2, provides the necessary centripedal force, m1·v^2 / r, needed for circular motion. Assuming G = 1 and m1 (the large mass) = 1, the radius of the orbit will be 1 and the velocity will be 1.
If the satellite's velocity, vp, is suddenly increased, its orbit will become elliptical. The intial radius (periapsis), rp, will be 1, but then the satellite will both slow down (to va) and move out to a maximum radius (apoapsis), ra = vp^2 / (2 - vp^2). However, if the velocity increased by a factor of sqrt(2) or more, the satellite will escape from orbit.

Expressed in terms of ra:
The formulas above use relative units, but it's easy to scale to realistic units. For example, to boost a satellite in low earth orbit (earth radius = 6378 km, escape velocity / sqrt(2) = 7.92 km/s) into geostationary orbit (42164 km). In relative units, ra = 42164 / 6378 = 6.611. The relative vp is sqrt( 2·6.611 / (6.611 + 1) ) = 1.318. So the LEO satellite velocity must increase by a factor of 1.318, to 10.44 km/s. Of course, the satellite will just reach geostationary orbit; it will follow its elliptical orbit back down unless its velocity is increased to maintain a circular orbit: v = 7.92 km/s / sqrt(6.611) = 3.08 km/s. As a check, geostationary velocity is 2 pi · 42164 km / (24 · 3600 s) = 3.07 km/s