Ferguson plots were first published by Kenneth A. Ferguson when he analyzed hormones of the pituitary gland in starch gels (Fig.3 and Equation 1 of article published in Metabolism 13, 985-1002 (1964)). The Ferguson plot is the semi-logarithmic plot of electrophoretic mobility vs. gel concentration. Please read on for a detailed explanation.
Gel electrophoresis is usually performed at one single gel concentration. Migration distances of sample zones are compared with the position of standards and the molecular size of unknowns is determined. This works fine with many applications. The procedure that we introduce here is not meant to replace routine procedures for examining hundreds of samples per day. It rather focuses on advanced operations sometimes necessary to arrive at correct results.
Gel electrophoresis depends on both particle size and surface net charge density. Determining particle sizes in ONE gel will only work, if the sample and standards have the SAME charge. This is usually true for nucleic acids and SDS denatured proteins. If not so, the "single gel - one lane of standards method" can be compared with solving one equation (migration distance) with two unknowns (size and charge). Depending on the setting, one can determine almost any size that is desired. Errors are also possible if sample and standards are of different nature, i.e., vary in conformation. This phenomenon is called anomalous migration or peak inversion in the literature, but it is nothing else than comparing, e.g., apples and bananas.
Often it is useful to exploit differences in both charge and size. Or one would like to investigate native samples, such as intact viruses, vesicles, etc. Or we know that the conformation varies, i.e., that we have linear and circular DNA. In all these cases we can apply the Ferguson plot method which allows to distinguish different particle shapes, sizes and surface net charge densities at the same time.
Since we ask for more information, it is necessary to provide more input data. We have to study the migration of particles not at one, but SEVERAL gel concentrations. Particle migration is measured as mobility.
Then we can generate the plot of log(mobility) vs. gel concentration (Ferguson plot), as shown in Fig. 1 below. Please see also related information about the Ogston model.
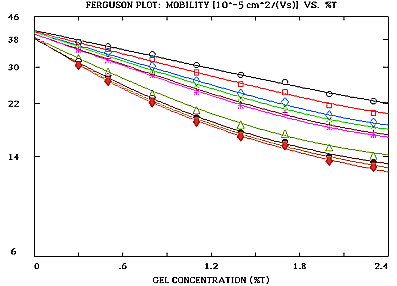
Fig. 1: Capillary electrophoresis of DNA fragments in liquid agarose as published in Electrophoresis 13, 286-294 (1992). The plot was generated by program ElphoFit (plot size reduced).
The Ferguson plot will be linear or nonlinear depending on the problem at hand. The plot may be evaluated by program ElphoFit. It uses file input. The output consists of graphics and tables providing statistical information. Part of the output are the size and free mobility (mobility in the absence of a gel, related to surface net charge density) of unknown particles. The size is determined in terms of effective molecular radii. The program allows to convert these radii to values of molecular (or particle) weight in Dalton or base pairs (bp). Parameters descriptive of the gel matrix are also specified. The slope of linear Ferguson plots is proportional to particle size. The intercept on the ordinate specifies particle free mobility. Particles of similar size have parallel Ferguson plots. Particles with the same surface net charge density have the same intercept on the log(mobility) axis (ordinate). This way, charge and size isomers can easily be detected.
Non-spherical particles produce nonlinear Ferguson plots. Nonlinearity may also occur, if gel matrix parameters vary with gel concentration. The slope of nonlinear plots close to 0 gel concentration is related to particle size. Size estimates are usually pretty good, even if differently shaped Ferguson plots are compared that originate from particles of different conformation.
Summarizing: The Ferguson plot method is more laborious, but yields more information and is capable of detecting anomalies which would remain undetected on a SINGLE gel. Sharp bands on a single gel do not necessarily warrant correct results.
Further information and literature are provided in the Readme files of the ElphoFit software package. Please address suggestions and further questions to:
Dietmar Tietz, Email: djt@his.com